A meter is defined as the distance traveled by light in 3 billionths of second. A second is defined as the time it takes for about 9 billion cycles of radiation of the cesium atom. But the definition of the kilogram is a little bit more approachable: it’s literally the mass of a particular chunk of metal in Paris called the International Prototype Kilogram (IPK). And even though it’s easier to understand, having an artifact as a definition comes with its own particular set of challenges. Measurements are so important to us, they have their own specific branch of science: metrology. And metrologists have come up with a pretty clever way of redefining the kilogram.

The kilogram is the only SI base unit currently defined by an artifact instead of a fundamental physical constant. But the kilo is part of the definition of twenty other units, including three other base units. It shows up in Amp, the Watt, the Newton, the Joule, the Candela, the Ohm, the lumen, lux, and mole, not to mention any of the imperial units which are officially defined based on their metric equivalents. In other words, basically the entire world’s system of measurements can be traced back to this single object in a vault in France. And you know they gave it a another bell jar just to make sure it was extra safe.

Here’s the issue: We made lots copies of the IPK to be used around the world, and we periodically hold kilogram reunions, so to speak, where all the facsimiles come back together for comparison. And despite our utmost diligence and care, it seems that the mass of each copy is drifting over time, gaining or losing fractions of a gram probably due to handling and/or long-term exposure to air. But one of the masses hasn’t changed: the IPK. Not because it has the same mass as it started with, but because it is literally the definition of a kilogram. You can put it on one side of the scale, but there’s nothing to put on the other side. The metrologists take a look at the IPK and say, “Yep, it’s still exactly a kilogram,” because it’s what a kilogram is. But the inconvenient truth is that all its copies are changing in mass over time, so we are pretty confident that the IPK is too. The linchpin of our entire system of measurements has some wiggle room that is impossible to characterize, because there’s nothing more constant to compare it to. And I'm just paraphrasing here, but that’s bad. So, scientists are working to redefine the kilogram to be based on a fundamental physical constant, and they’ve come up with a pretty cool way to accomplish this: the watt balance.

Fundamentally, the watt balance is a scale that uses an electromagnetic force to balance the weight of the mass it’s measuring. But, it has a trick up its sleeve that allows it to measure with extreme accuracy and precision. I built a model to help illustrate how it works. This watt balance is based on a design created by a few scientists at the US National Institute of Standards and Technology. I really like the juxtaposition of a precision scientific instrument made with a natural material, so I made it out of wood. And I made a separate video all about how this was built.

Before we reveal the secret to the watt balance’s extreme precision, we need to perform the initial alignment and calibration, which is a perfect opportunity to show the different parts of the model. At first glance, the watt balance looks like a standard beam balance you’d see in a classroom or in practically any motif related to justice. But you’re looking at a sophisticated scientific device capable of measuring to within an error of approximately 1%, or at least that’s what the scientists said. The real watt balances have accuracies up to 2 parts in 100 million.

Each of the two platforms includes a wound coil of wire. The platforms are hollow so that they can move freely up and down around a pair of opposing permanent magnets on each side. To measure the position of the arm, the watt balance uses a shadow sensor which consists of a photodiode and a laser line. As the balance moves, it gradually obstructs the path of the laser, changing the intensity of light hitting the sensor. Another laser on top of the arm provides an optical lever for calibration. A small movement of the arm creates a large movement of the laser dot on an adjacent wall. By measuring the distance the optical lever moves for a few different arm positions, and comparing those to the corresponding readings from the shadow sensor, we can calibrate the watt balance so it knows the precise position of its arm.

Now we can start measuring. The secret to the watt balance’s extreme precision is its dual mode operation which utilizes some interesting properties of electromagnetism. In the first mode, the watt balance applies a current to one of the coils around the platform, creating an electromagnet. The coil reacts to the existing magnetic field, generating an upward force, also known as the LaPlace force. This setup is similar to how many electric motors work: applying a current to a coil of wire within a magnetic field. The control software written by the NIST scientists includes a PID control algorithm that can do this automatically, but I just manually adjust the current in the coil using my bench power supply until the upward force is exactly equal to the weight of the object. I do this once with no object, once with the object, and then once again without it to get an accurate value of just the current required to balance the object alone.

Let’s take a look at this system expressed as an equation. The weight of the object is simply its mass times the gravitational acceleration. The LaPlace force is the product of the magnetic field strength of the permanent magnets, the length of the wire in the coil, and current in the coil. If the beam is static, that means the two forces are equal. Remember, our goal is to find the mass of the object. We can measure gravity and current to very high accuracy, but length of the coil and especially the magnetic field strength are very difficult to measure with extreme accuracy. Without those values, we can’t solve this equation for mass… yet.

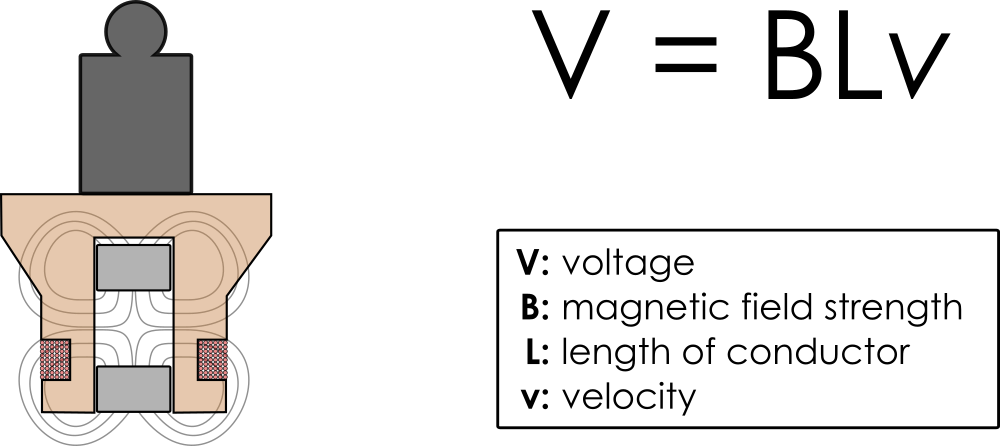
This is where the ingenuity of the watt balance comes into play. You may know that many electric motors can be used in reverse to generate electricity if you apply a mechanical input force. In other words, the electromagnetic principle is reversible. Apply an electromotive force and you get a mechanical force out. Apply a mechanical force, and you get an electromotive force out. The watt balance takes advantage of this for its second mode of operation. Instead of applying a current to the coil, we simply move it through the magnetic field. We know from Faraday’s Law of Induction, when you move a conductor through a magnetic field, you generate a voltage. This is the reason our watt balance has two coils. Applying a varying current to coil B moves the beam in an up and down motion. The shadow sensor measures the velocity of the this motion, and we also measure the voltage induced in the coil A. The software samples both the voltage and velocity as the coil moves through the magnetic field.

From Faraday’s law, we know the voltage is equal to the product of velocity, magnetic field strength, and the length of the conductor. Remember from the first mode that we couldn’t accurately measure the magnetic field strength or the precise length of the conductor, but we’re using the same coil around the same pair of permanent magnets. In other words, even though we don’t know what they are, we do know that these two variables (B and L) are exactly the same in both equations. As the software samples the velocity and voltage, it generates a best fit line. The slope of this line represents the quantity of this BL that we couldn’t measure directly. With a little bit of algebra we can rearrange these equations and perform a substitution to completely eliminate those variables: VI = mgv. And take a look at the units: Current times voltage is power, and force times velocity is power. Both are measured in watts, hence the name of the instrument.

Rearranging a bit more, now we have an equation for mass which only consists of the parameters we’re capable of measuring accurately: m = VI/gv. We measured the current required to hold up the object in the first mode. Then we measured the voltage over velocity in the second mode. We know the acceleration due to earth’s gravity, so we have everything we need to determine the mass of the object. It’s so simple that you almost don’t notice how big of a deal this really is. Traditionally, an instrument that measures mass would be calibrated using known artifacts that themselves were calibrated using known artifacts and so on and so on in a chain all the way back to the IPK, but I haven’t done any of that. I know this mass is about 20 grams because it says so right on top, but if I didn’t know that and had nothing to compare it to, I could still get an accurate measurement out of the watt balance. And here’s the most important part: Since voltage and current are defined in terms of fundamental physical constants, the watt balance makes it possible to define the kilogram in terms of these absolutes, eliminating the need for a physical artifact.

Trace them back far enough and you’ll find that all measurements are relative, they’re a comparison. Sometimes a comparison to something immutable, but in the case of the kilogram, not yet. Redefining the kilogram to be based on a fundamental physical constant means not only that we have more confidence in our measurements, but it also makes metrology more democratic by metaphorically setting the standard free from its vault and bell jars so that anyone with a garage workshop and a little bit too much free time has access. Measurements are the language of science engineering and metrology makes sure that we’re all speaking the same one. Thank you for watching, and let me know what you think!